Astructure that is composed of a number of bars pin connected at their ends to form a stable framework is called a truss. It is generally assumed that loads and reactions are applied to the truss only at the joints. A truss would typically be composed of triangular elements with the bars on the upper chord under compression and those along the lower chord under tension. Trusses are extensively used for bridges, long span roofs, electric tower, and space structures.
Trusses are statically determinate when the entire bar forces can be determined from the equations of statics alone. Otherwise the truss is statically indeterminate. A truss may be statically (externally) determinate or indeterminate with respect to the reactions (more than 3 or 6 reactions in 2D or 3D problems respectively).
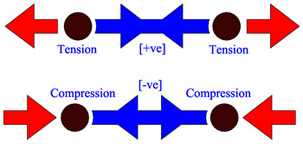
Members subjected to forces; Tension and Compression.
For trusses analysis, it is assumed that:
Bars are pin-connected.
Joints are frictionless hinges.
Loads are applied at the joints only.
Stress in each member is constant along its length.
The objective of analyzing the trusses is to determine the reactions and member forces. The methods used for carrying out the analysis with the equations of equilibrium and by considering only parts of the structure through analyzing its free body diagram to solve the unknowns.
Trusses are statically determinate when the entire bar forces can be determined from the equations of statics alone. Otherwise the truss is statically indeterminate. A truss may be statically (externally) determinate or indeterminate with respect to the reactions (more than 3 or 6 reactions in 2D or 3D problems respectively).
Members subjected to forces; Tension and Compression.
For trusses analysis, it is assumed that:
Bars are pin-connected.
Joints are frictionless hinges.
Loads are applied at the joints only.
Stress in each member is constant along its length.
The objective of analyzing the trusses is to determine the reactions and member forces. The methods used for carrying out the analysis with the equations of equilibrium and by considering only parts of the structure through analyzing its free body diagram to solve the unknowns.
Method of Joints :
The first to analyze a truss by assuming all members are in tension reaction. A tension member is when a member experiences pull forces at both ends of the bar and usually denoted as positive (+ve) sign. When a member experiencing a push force at both ends, then the bar was said to be in compression mode and designated as negative (-ve) sign.
In the joints method, a virtual cut is made around a joint and the cut portion is isolated as a Free Body Diagram (FBD). Using the equilibrium equations of ∑ Fx = 0 and ∑ Fy = 0, the unknown member forces could be solve. It is assumed that all members are joined together in the form of an ideal pin, and that all forces are in tension (+ve) of reactions.
An imaginary section may be completely passed around a joint in a truss. The joint has become a free body in equilibrium under the forces applied to it. The equations ∑ H = 0 and ∑ V = 0 may be applied to the joint to determine the unknown forces in members meeting there. It is evident that no more than two unknowns can be determined at a joint with these two equations.
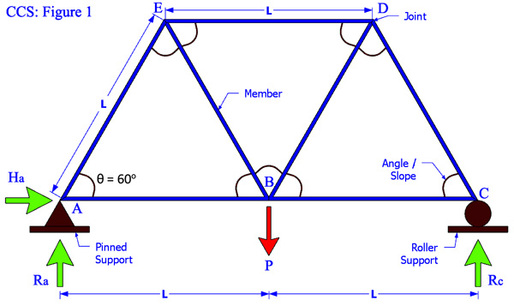
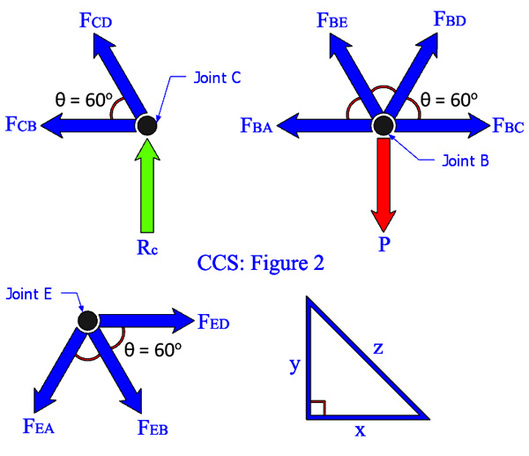
Figure 1: A simple truss model supported by pinned and roller support at its end. Each triangle has the same length, L and it is equilateral where degree of angle, θ is 60° on every angle. The support reactions, Ra and Rc can be determine by taking a point of moment either at point A or point C, whereas Ha = 0 (no other horizontal force).
Here are some simple guidelines for this method:
Firstly draw the Free Body Diagram (FBD),
Solve the reactions of the given structure,
Select a joint with a minimum number of unknown (not more than 2) and analyze it with ∑ Fx = 0 and ∑ Fy = 0,
Proceed to the rest of the joints and again concentrating on joints that have very minimal of unknowns,
Check member forces at unused joints with ∑ Fx = 0 and ∑ Fy = 0,
Tabulate the member forces whether it is in tension (+ve) or compression (-ve) reaction.
Here are some simple guidelines for this method:
Firstly draw the Free Body Diagram (FBD),
Solve the reactions of the given structure,
Select a joint with a minimum number of unknown (not more than 2) and analyze it with ∑ Fx = 0 and ∑ Fy = 0,
Proceed to the rest of the joints and again concentrating on joints that have very minimal of unknowns,
Check member forces at unused joints with ∑ Fx = 0 and ∑ Fy = 0,
Tabulate the member forces whether it is in tension (+ve) or compression (-ve) reaction.
Figure 2: The figure showing 3 selected joints, at B, C, and E. The forces in each member can be determine from any joint or point. The best way to start by selecting the easiest joint like joint C where the reaction Rc is already obtained and with only 2 unknown, forces of FCB and FCD. Both can be evaluate with ∑ Fx = 0 and ∑ Fy = 0 rules. At joint E, there are 3 unknown, forces of FEA, FEB and FED, which may lead to more complex solution compare to 2 unknown values. For checking purposes, joint B is selected to shown that the equation of ∑ Fx is equal to ∑ Fy which leads to zero value, ∑ Fx = ∑ Fy = 0. Each value of the member’s condition should be indicate clearly as whether it is in tension (+ve) or in compression (-ve) state.
Trigonometric Functions:
Taking an angle between member x and z…
Cos θ = x / z
Sin θ = y / z
Tan θ = y / x
Method of Sections :
The section method is an effective method when the forces in all members of a truss are being able to determine. Often we need to know the force in just one member with greatest force in it, and the method of section will yield the force in that particular member without the labor of working out the rest of the forces in the truss.
If only a few member forces of a truss are needed, the quickest way to find these forces is by the method of sections. In this method, an imaginary cutting line called a section is drawn through a stable and determinate truss. Thus, a section subdivides the truss into two separate parts. Since the entire truss is in equilibrium, any part of it must also be in equilibrium. Either of the two parts of the truss can be considered and the three equations of equilibrium ∑ Fx = 0, ∑ Fy = 0, and ∑ M = 0 can be applied to solve for member forces.
Trigonometric Functions:
Taking an angle between member x and z…
Cos θ = x / z
Sin θ = y / z
Tan θ = y / x
Method of Sections :
The section method is an effective method when the forces in all members of a truss are being able to determine. Often we need to know the force in just one member with greatest force in it, and the method of section will yield the force in that particular member without the labor of working out the rest of the forces in the truss.
If only a few member forces of a truss are needed, the quickest way to find these forces is by the method of sections. In this method, an imaginary cutting line called a section is drawn through a stable and determinate truss. Thus, a section subdivides the truss into two separate parts. Since the entire truss is in equilibrium, any part of it must also be in equilibrium. Either of the two parts of the truss can be considered and the three equations of equilibrium ∑ Fx = 0, ∑ Fy = 0, and ∑ M = 0 can be applied to solve for member forces.
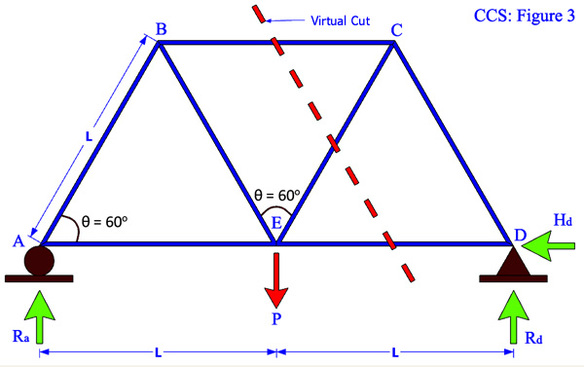
Figure 3: Using the same model of simple truss, the details would be the same as previous figure with 2 different supports profile. Unlike the joint method, here we only interested in finding the value of forces for member BC, EC, and ED.
Few simple guidelines:
Pass a section through a maximum of 3 members of the truss, 1 of which is the desired member where it is dividing the truss into 2 completely separate parts,
At 1 part of the truss, take moments about the point (at a joint) where the 2 members intersect and solve for the member force, using ∑ M = 0,
Solve the other 2 unknowns by using the equilibrium equation for forces, using ∑ Fx = 0 and ∑ Fy = 0.
Note: The 3 forces cannot be concurrent, or else it cannot be solve.
Few simple guidelines:
Pass a section through a maximum of 3 members of the truss, 1 of which is the desired member where it is dividing the truss into 2 completely separate parts,
At 1 part of the truss, take moments about the point (at a joint) where the 2 members intersect and solve for the member force, using ∑ M = 0,
Solve the other 2 unknowns by using the equilibrium equation for forces, using ∑ Fx = 0 and ∑ Fy = 0.
Note: The 3 forces cannot be concurrent, or else it cannot be solve.
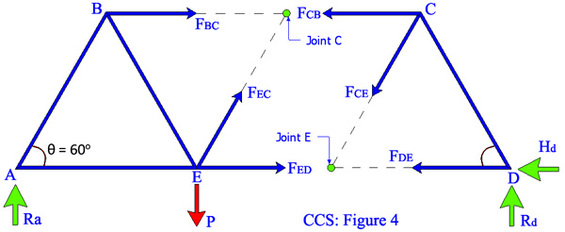
Figure 4: A virtual cut is introduce through the only required members which is along member BC, EC, and ED. Firstly, the support reactions of Ra and Rd should be determine. Again a good judgment is require to solve this problem where the easiest part would be consider either on the left hand side or the right hand side. Taking moment at joint E (virtual pint) on clockwise for the whole RHS part would be much easier compare to joint C (the LHS part). Then, either joint D or C can be consider as point of moment, or else using the joint method to find the member forces for FCB, FCE, and FDE. Note: Each value of the member’s condition should be indicate clearly as whether it is in tension (+ve) or in compression (-ve) state.