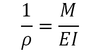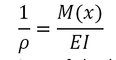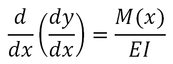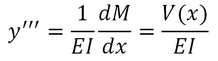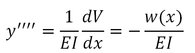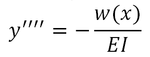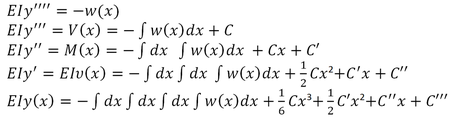Introduction
In the preceding chapter we learned to design beams for strength. In this chapter we will be concerned with another aspect in the design of beams, namely, the determination of deflection. Of particular interest is the determination of the maximum deflection of a beam under a given loading, since the design specifications of a beam will generally include a maximum allowable value for its deflection. Also of interest is that the knowledge of the deflections is required to analyze indeterminate beams. These are beams in which the number of reactions at the support exceeds the number of equilibrium equations available to determine these unknowns.
We saw before that a prismatic beam subjected to pure bending is bent into an arc of circle and that, within the elastic rang, the curvature of the neutral surface can be expressed as
We saw before that a prismatic beam subjected to pure bending is bent into an arc of circle and that, within the elastic rang, the curvature of the neutral surface can be expressed as
Where M is the bending moment, E is the modulus of elasticity, and the moment of inertia of the cross section about its neutral axis.
When a beam is subjected to transverse loading, remains valid for any given transverse section, provided that Saint-Venant’s principle applies. However, both the bending moment and the curvature of the neutral surface will vary from section to section. Denoting by the distance of the section from the left end of the beam, we write
When a beam is subjected to transverse loading, remains valid for any given transverse section, provided that Saint-Venant’s principle applies. However, both the bending moment and the curvature of the neutral surface will vary from section to section. Denoting by the distance of the section from the left end of the beam, we write
The knowledge of the curvature at various points of the beam will enable us to draw some general conclusions regarding the deformation of the beam under loading
To determine the slope and deflection of the beam at any given point, we first derive the following second-order linear differential equation, which governs the elastic curve characterizing the shape of the deformed beam
To determine the slope and deflection of the beam at any given point, we first derive the following second-order linear differential equation, which governs the elastic curve characterizing the shape of the deformed beam
Where is the bending moment in the beam. We now recall from RELATIONS AMONG LOAD, SHEAR, AND BENDING MOMENT that when a beam supports a distributed load , we have and at any point of the beam. Differentiating both members of the last equation w.r.t. and assuming to be constant. We have therefore
And, differentiate again,
We conclude that, when a prismatic beam supports a distributed load , its elastic curve is governed by the fourth-order linear differential equation
Multiplying both members of the last equation by the constant and integrating four times, we write
This means that you have to integrate four times , sound like fun !