The equilibrium of a body is expressed as
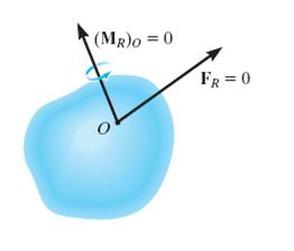
FR=∑F=0 , (∑MR)o=∑Mo=0
Consider summing moments about some other point, such as point A, we require
∑MA= r X FR +(MR)O=0
For equilibrium of a rigid body in 2D,
ΣFx= 0; ΣFy= 0; ΣMO= 0
•ΣFxand ΣFyrepresent sums of x and y components of all the forces
•ΣMOrepresents the sum of the couple moments and moments of the force components
Consider summing moments about some other point, such as point A, we require
∑MA= r X FR +(MR)O=0
For equilibrium of a rigid body in 2D,
ΣFx= 0; ΣFy= 0; ΣMO= 0
•ΣFxand ΣFyrepresent sums of x and y components of all the forces
•ΣMOrepresents the sum of the couple moments and moments of the force components
Free Body Diagrams- Support Reactions:
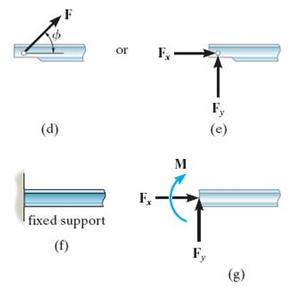
• If a support prevents the translation of a body in a given direction, then a force is developed on the body in that direction.
• If rotation is prevented, a couple moment is exerted on the body.
• If rotation is prevented, a couple moment is exerted on the body.
Free Body Diagrams-Internal Forces:
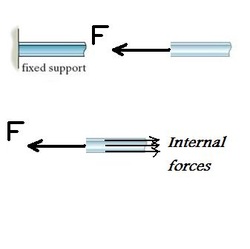
•External and internal forces can act on a rigid body
•For FBD, internal forces act between particles which are contained within the boundary of the FBD, are not represented
•Particles outside this boundary exert external forces on the system
Weight and Center of Gravity
•Each particle has a specified weight
•System can be represented by a single resultant force, known as weight Wof the body
•Location of the force application is known as the center of gravity
Procedure for Drawing a FBD:
1. Draw Outlined Shape
•Imagine body to be isolated or cut free from its constraints
2. Show All Forces and Couple Moments
•Identify all external forces and couple moments that act on the body
Procedure for Analysis
Equations of Equilibrium
•Apply ΣMO= 0 about a point O
•Unknowns moments of are zero about O and a direct solution the third unknown can be obtained
•Orient the x and y axes along the lines that will provide the simplest resolution of the forces into their x and y components
•Negative result scalar is opposite to that was assumed on the FBD
•For FBD, internal forces act between particles which are contained within the boundary of the FBD, are not represented
•Particles outside this boundary exert external forces on the system
Weight and Center of Gravity
•Each particle has a specified weight
•System can be represented by a single resultant force, known as weight Wof the body
•Location of the force application is known as the center of gravity
Procedure for Drawing a FBD:
1. Draw Outlined Shape
•Imagine body to be isolated or cut free from its constraints
2. Show All Forces and Couple Moments
•Identify all external forces and couple moments that act on the body
Procedure for Analysis
Equations of Equilibrium
•Apply ΣMO= 0 about a point O
•Unknowns moments of are zero about O and a direct solution the third unknown can be obtained
•Orient the x and y axes along the lines that will provide the simplest resolution of the forces into their x and y components
•Negative result scalar is opposite to that was assumed on the FBD
