Equilibrium :
analysisThe Course is mainly based on equilibrium which is defined as Summation of all forces and moments equals zero ,and in case of structure analysis it means that a structure will be able to sustain all external loads ,and its internal force can handle the external pressure.
Course Objectives :
•Develop the equations of equilibrium for a rigid body
•Concept of the free-body diagram for a rigid body
•Solve rigid-body equilibrium problems using the equations of equilibrium
When all the forces that act upon an object are balanced, then the object is said to be in a state of equilibrium.
If an object is at equilibrium, then the forces are balanced. Balanced is the key word that is used to describe equilibrium situations. Thus, the net force is zero and the acceleration is 0 m/s/s. Objects at equilibrium must have an acceleration of 0 m/s/s. This extends from Newton's first law of motion. But having an acceleration of 0 m/s/s does not mean the object is at rest. An object at equilibrium is either ...
at rest and staying at rest, or
in motion and continuing in motion with the same speed and direction.
If an object is at rest and is in a state of equilibrium, then we would say that the object is at "static equilibrium." "Static" means stationary or at rest.
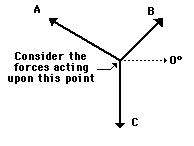
The state of the object is analyzed in terms of the forces acting upon the object.The object is a point on a string upon which three forces were acting. See diagram at right. If the object is at equilibrium, then the net force acting upon the object should be 0 Newton. Thus, if all the forces are added together as vectors, then the resultant force (the vector sum) should be 0 Newton. (Recall that the net force is "the vector sum of all the forces" or the resultant of adding all the individual forces head-to-tail.) Thus, an accurately drawn vector addition diagram can be constructed to determine the resultant. Sample data for such a lab are shown below.
Course Objectives :
•Develop the equations of equilibrium for a rigid body
•Concept of the free-body diagram for a rigid body
•Solve rigid-body equilibrium problems using the equations of equilibrium
When all the forces that act upon an object are balanced, then the object is said to be in a state of equilibrium.
If an object is at equilibrium, then the forces are balanced. Balanced is the key word that is used to describe equilibrium situations. Thus, the net force is zero and the acceleration is 0 m/s/s. Objects at equilibrium must have an acceleration of 0 m/s/s. This extends from Newton's first law of motion. But having an acceleration of 0 m/s/s does not mean the object is at rest. An object at equilibrium is either ...
at rest and staying at rest, or
in motion and continuing in motion with the same speed and direction.
If an object is at rest and is in a state of equilibrium, then we would say that the object is at "static equilibrium." "Static" means stationary or at rest.
The state of the object is analyzed in terms of the forces acting upon the object.The object is a point on a string upon which three forces were acting. See diagram at right. If the object is at equilibrium, then the net force acting upon the object should be 0 Newton. Thus, if all the forces are added together as vectors, then the resultant force (the vector sum) should be 0 Newton. (Recall that the net force is "the vector sum of all the forces" or the resultant of adding all the individual forces head-to-tail.) Thus, an accurately drawn vector addition diagram can be constructed to determine the resultant. Sample data for such a lab are shown below.
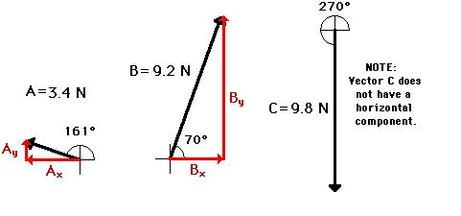
Another way of determining the net force (vector sum of all the forces) involves using the trigonometric functions to resolve each force into its horizontal and vertical components. Once the components are known, they can be compared to see if the vertical forces are balanced and if the horizontal forces are balanced. The diagram below shows vectors A, B, and C and their respective components. For vectors A and B, the vertical components can be determined using the sine of the angle and the horizontal components can be analyzed using the cosine of the angle. The magnitude and direction of each component for the sample data are shown in the table below the diagram.
structe
structe
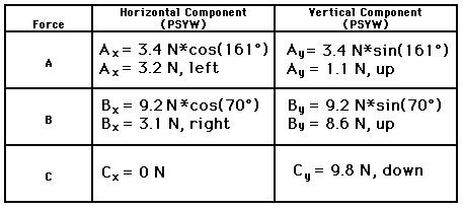
The data in the table above show that the forces nearly balance. An analysis of the horizontal components shows that the leftward component of A nearly balances the rightward component of B. An analysis of the vertical components show that the sum of the upward components of A + B nearly balance the downward component of C. The vector sum of all the forces is (nearly) equal to 0 Newton. But what about the 0.1 N difference between rightward and leftward forces and the 0.2 N difference between the upward and downward forces? Why do the components of force only nearly balance? The sample data used in this analysis are the result of measured data from an actual experimental setup. The difference between the actual results and the expected results is due to the error incurred when measuring force A and force B. We would have to conclude that this low margin of experimental error reflects an experiment with excellent results. We could say it's "close enough for government work."