Poisson’s Ratio :
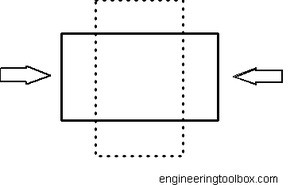
When a material is stretched with an axial load in one direction it gets thinner in the other two perpendicular directions, the ratio between the longitudinal strain and transverse strain is called Poisson’s ratio.
Poisson's ratio, also called the Poisson coefficient, is the ratio of transverse contraction strain to longitudinal extension strain in a stretched bar. Since most common materials become thinner in cross section when stretched, Poisson's ratio for them is positive. The reason is that inter-atomic bonds realign with deformation. Stretching of normal honeycomb, shown on the right, illustrates the concept. Normal polymer foams or cellular solids, above left, have a positive Poisson's ratio. Re-entrant polymer foams developed in our laboratory, above right, have a negative Poisson's ratio. After our original article appeared in Science, they were called anti-rubber by James Glieck of the New York Times, and were called auxetic (or auxetics, or auxetic materials) by K. Evans and co-workers in Exeter, England, and F. Scarpa and co-workers in Bristol, England, and were called dilational by mathematician Graeme Milton of the University of Utah. Negative Poisson's ratio chiral honeycomb, above center, unrolls when stretched. Click on the image for the article. Negative Poisson's ratio re-entrant honeycomb, below right, unfolds when stretched.
Poisson's Ratio can be expressed as
υ = - εt / εl (1)
where
υ = Poisson's ratio
εt = transverse strain
εl = longitudinal or axial strain
Strain can be expressed as
ε = dl/L (2)
where
dl = change in length
L = initial length
For most common materials the Poisson's ratio is in the range 0 - 0.5.
Poisson's ratio, also called the Poisson coefficient, is the ratio of transverse contraction strain to longitudinal extension strain in a stretched bar. Since most common materials become thinner in cross section when stretched, Poisson's ratio for them is positive. The reason is that inter-atomic bonds realign with deformation. Stretching of normal honeycomb, shown on the right, illustrates the concept. Normal polymer foams or cellular solids, above left, have a positive Poisson's ratio. Re-entrant polymer foams developed in our laboratory, above right, have a negative Poisson's ratio. After our original article appeared in Science, they were called anti-rubber by James Glieck of the New York Times, and were called auxetic (or auxetics, or auxetic materials) by K. Evans and co-workers in Exeter, England, and F. Scarpa and co-workers in Bristol, England, and were called dilational by mathematician Graeme Milton of the University of Utah. Negative Poisson's ratio chiral honeycomb, above center, unrolls when stretched. Click on the image for the article. Negative Poisson's ratio re-entrant honeycomb, below right, unfolds when stretched.
υ = - εt / εl (1)
where
υ = Poisson's ratio
εt = transverse strain
εl = longitudinal or axial strain
Strain can be expressed as
ε = dl/L (2)
where
dl = change in length
L = initial length
For most common materials the Poisson's ratio is in the range 0 - 0.5.
Volumetric Strain:
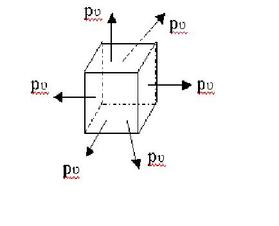
In volumetric strain, strains in all directions are equal :
ε=εx=εy=εz=T/E (1-2σ)
εt=3 T/E (1-2σ)
εt≠0
Thus, (1-2σ) ≥0
2σ≤1
ε=εx=εy=εz=T/E (1-2σ)
εt=3 T/E (1-2σ)
εt≠0
Thus, (1-2σ) ≥0
2σ≤1
